# 【算法】斐波那契数列的概念

# 斐波那契数列的概念

​ 斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多・斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为 “兔子数列”。

​ 斐波那契数列指的是这样一个数列：

​ 0，1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987，1597，2584，4181，6765，10946，17711……

​ 它的规律是：这个数列从第 3 项开始，每一项都等于前两项之和。

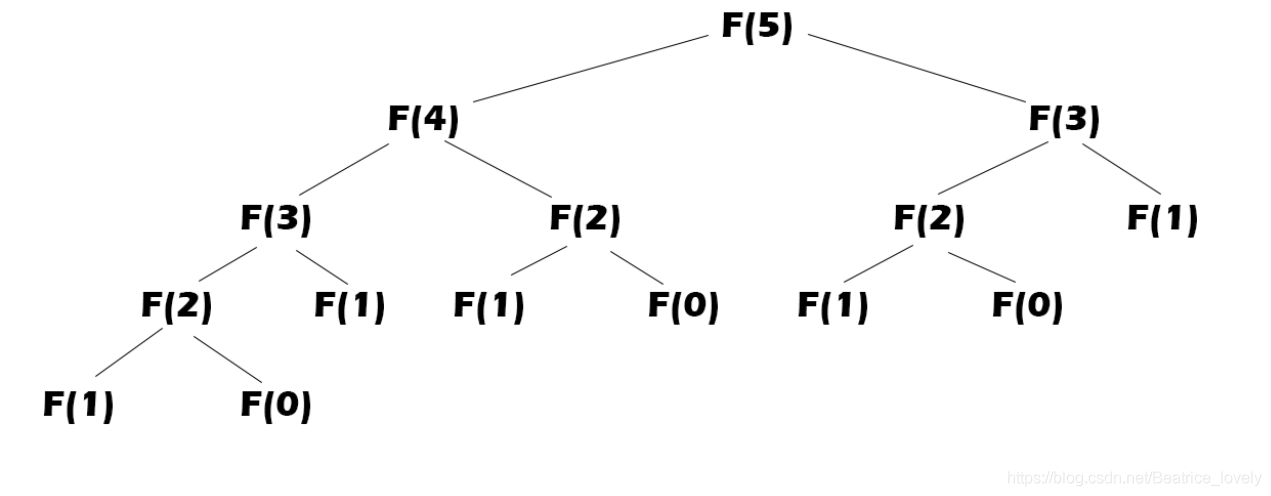
​ 在数学上，斐波那契数列以如下被以递推的方法定义：F*(0)=0，*F*(1)=1, *F*(n)=*F*(n - 1)+*F*(n - 2)（*n* ≥ 2，*n* ∈ N*），显然，斐波那契数列是一个线性递推数列 *。

---

# 斐波那契数列的实现

​ 常用的实现斐波那契数列的方法分为两大类：递归和循环。

# 1. 递归实现

#include <stdio.h>
int F(int n) //斐波那契数列函数 递归形式
{
    if(n == 0) //初始化
		return 0;
	if(n == 1 || n == 2)
		return 1;
    return F(n-1) + F(n-2);  //如果n != 1 && n != 2 进行递归运算
}
 
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
    	scanf("%d",&n);
    	printf("%d\n", F(n));
	}
    return 0;
}

---

# 2. 迭代实现（优先使用）

# 6091: 斐波那契数列

#include <stdio.h>
int fibonacci(int n) //定义斐波那契函数
{
    if(n == 0)	 //定义初始值
        return 0;   
    if(n == 1 || n == 2)	
        return 1;
    int a=1,b=1,c=0;    //定义初始值
//用一个for循环，a、b分别为前两项，c为前两项之和，得到c后进行交换更新a、b的值，进行n次交换即可。
    for(int i=3;i<=n;i++)    //更新操作
    {
    	c = a+b;
    	a = b;
    	b = c;
	}
	return c;  //c即为结果输出
}
 
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
    	scanf("%d",&n);
    	printf("%d\n", fibonacci(n));
	}
    return 0;
}

---

​ 递归和迭代的改进算法可以参考 ** 微 光的斐波那契数列 **。

​ 因为递归算法存在着大量的重复计算，在 N 趋近于较大值时，可能会造成内存溢出或超时的情况，又因为使用迭代算法的情况下同样可以实现计算斐波那契数列第 N 项的功能，所以在 N 值很大时我们优先使用迭代算法。

---

# 斐波那契数列的应用

• 10 个连续的斐波那契数的和 = 第 7 个数的 11 倍
• 前 n 项和 = 第 n + 2 项 - 第 2 项
• 从第 2 项开始，第 2n - 1 项的平方比 2n * (2n - 2) 多 1；第 2n 项的平方比 2n * (2n - 2) 少 1。

# 1**. 黄金分割 **

** 黄金分割：** 把任一线段分割成两段，使 大段 / 全段 = 小段 / 大段， 比值经过计算之后，就是黄金分割比。

​ 斐波那契数列：随着数列项数的增加，前一项与后一项之比越来越逼近 ** 黄金分割 * 的数值 0.6180339887……***

​ 卢卡斯数列：斐波那契数列的推广形式，卢卡斯数列的形式为：1， 3， 4， 7， 11， 18，29，47…… 卢卡斯数列的相邻两项比值的极限恰好也是二分之根号五减一，即黄金分割比。所以说，卢卡斯抓住了斐波那契数列的本质。

#include<stdio.h>
int main()
{
	double f[100];
	f[1]=1, f[2]=1;
	for(int i=3; i<=50; i++)
	{
		f[i]=f[i-1]+f[i-2];
	}
	int n;
	scanf("%d",&n);
	printf("%.10lf\n",f[n]/f[n+1]);
 }

---

# 2. 杨辉三角

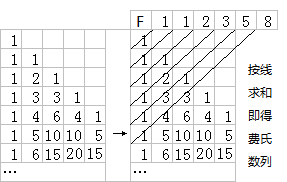
​ 如图所示作 45 度斜线，之后做直线的平行线，将每条直线所经过的数，即得之和即为斐波那契数列。

---

# 3. 兔子数列

​ * 斐波那契数列又因数学家 * 列昂纳多・斐波那契 * 以兔子繁殖为例子而引入，故又称为 “* 兔子数列 *”。***

​ **** 兔子数列是指：**** 一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

​ 很容易发现 “兔子数列” 问题和斐波那契数列问题相同，都是一样的解法。

# 1376: 母牛的故事

#include<stdio.h> 
void DataInit(int *a)
{
    for(int i = 4; i < 55; i++)
        a[i] = a[i-1] + a[i-3];
}
int main()
{
    int a[55] = {0, 1, 2, 3};
    int n;
    DataInit(a);
    while(scanf("%d", &n)!=EOF)
    if(n)
        printf("%ld\n", a[n]);
    else break;
    return 0;
}

---

# 4. 排列组合

​ 有一段楼梯，有 10 级台阶，规定每一步只能跨一级或两级，要登上第 10 级台阶有几种不同的走法？

​ 这也是一个斐波那契数列：

​ 登第一级台阶，有一种走法，0->1；

​ 登第二级台阶，有两种走法，0->1->2，0->2；

​ 登第三级台阶，有三种走法，0->1->2->3，0->1->3，0->2->3；

​ 登第四级台阶，有五种走法，0->1->2->3->4，0->1->2->4，0->1->3->4，0->2->3->4，0->2->4；

​ …

​ 即 1， 2， 3， 5， 8， 13，… 到 10 级，就是 89 种走法，与斐波那契数列的规律契合。

​ 类似的斐波那契数列的规律运用还有很多。

​ （1， 1， 2， 3， 5， 8， 13， 21， 33， 54， 89…）

# 5. 矩形面积

​ 右下图可知，斐波那契数列与矩形面积的生成相关。

​

​ 不难发现一个规律，即 ** 生成的矩形中，所有小正方形的面积之和等于大矩形的面积。** 即：

# 关于我

Brath 是一个热爱技术的 Java 程序猿，公众号「InterviewCoder」定期分享有趣有料的精品原创文章！

非常感谢各位人才能看到这里，原创不易，文章如果有帮助可以关注、点赞、分享或评论，这都是对我的莫大支持！